The Simon Research Ensemble
our research
we develop mathematical models, train machine learning models, and conduct simulations to tackle or deliver insights into problems in chemistry and materials science.
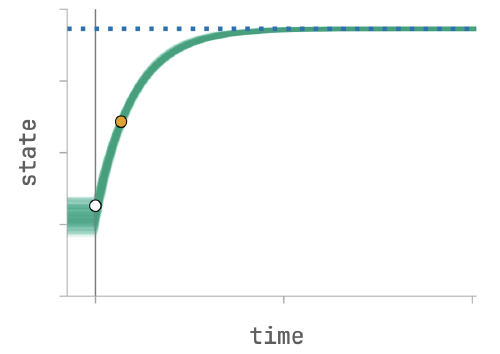
Bayesian statistical inversion
to solve inverse problems while quantifying uncertainty
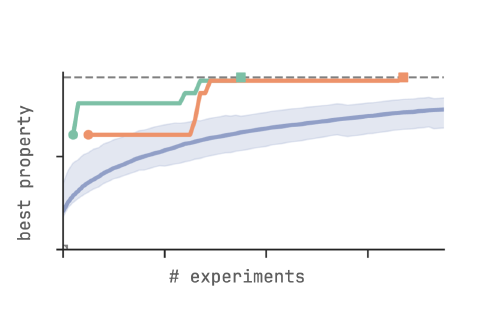
Bayesian optimization
to efficiently search for materials with optimal properties
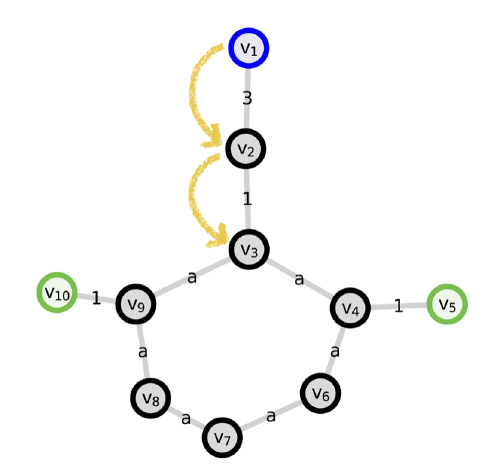
machine learning
to predict the properties of molecules and materials
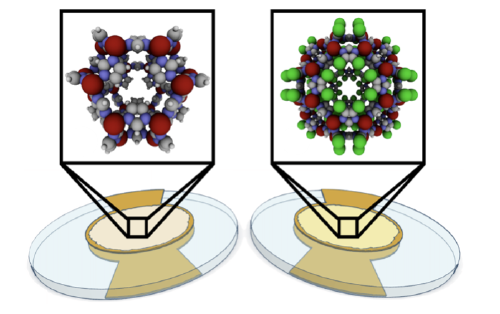
electronic noses
computational design; machine learning to interpret their response patterns
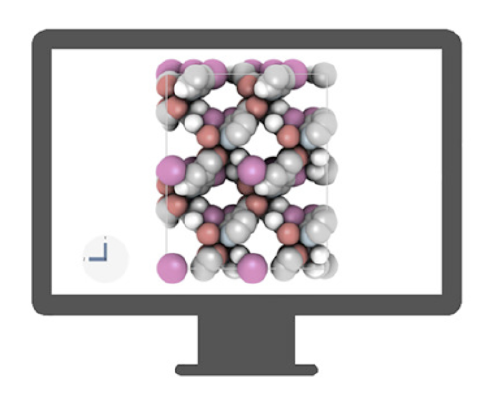
molecular simulation
to predict gas adsorption properties of nanoporous materials
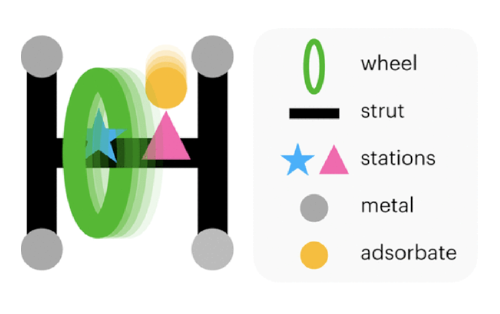
toy stat mech models
of adsorption in flexible, nanoporous crystals
we see mathematics, statistical mechanics, and machine learning as a toolbox to approach a variety of interesting problems. ie., we are at a buffet.
I think you can put scientists into two buckets. One is the type who dives very deeply into one topic for their whole career and they know it better than anybody else in the world. Then there’s the other bucket, where I would put myself, where it’s like you’re at a buffet table and you see an interesting thing here and do it for a while, and that connects you to another interesting thing and you take a bit of that. - Jennifer Doudna